Thursday, March 8. 2007
The Game of Life
How could life on earth be so diverse? How could earth, the solar system or even the universe be so complex? How could it be so without it all being made, designed exactly that way? Really, how could it?! It's a fair question and makes a lot of people wonder. But there ARE answers - some are definite some not-so-definite. After all, life (and the universe) IS pretty complex. However, the interesting thing with complexity is that, complexity doesn't mean that it is entirely irreducible or that it couldn't have arisen from something less complex.
Introduction
Enter John Conway's "The Game of Life" - one of the simplest examples of emergent complexity. The Game of Life (hereafter abbreviated to TGOL) is a type of cellular automata. Cellular Automata can be defined as a structure (cell) which has a finite set of states and any transitions from one state to another occur according to a set of predetermined rules. TGOL operates in a universe represented by a 2-dimensional grid - where the state of each cell in the grid is boolean; i.e. a cell is either alive or dead. The rules, in TGOL, simply determine the state of a cell at any given moment in time as per the states of the cells surrounding it. That's as much complexity as there is in TGOL (and many other Cellular Automata)!
It is quite intuitive to imagine this working at small scales for just a few steps in time but it quickly gets a bit too large a problem to work out in the head. In fact, TGOL can only be executed effectively using the massive computational abilities of a computer but even then, after sometime, the problem gets beyond which a computer can handle. What more, it is near impossible to determine the future state of the cells based on the starting states.
Experiment!
First, the "rules" in The Game of Life as defined by Conway.
- Any dead cell becomes alive if it has exactly 3 live neighbours.
- Any live cell with either 2 or 3 live neighbours stay alive.
- Any other case either kills the cell if it's alive or leaves it dead if it's already dead.
You can "play" TGOL on paper or simulate it on the computer. Being the lazy people we are, I have no doubt most of you would choose the latter option - but if you are any bit curious about TGOL, do try working it out manually first. There are many Life simulation programs available for free on the net - some are run online while some are available for download. Try the Java based Life simulator at http://www.ibiblio.org/lifepatterns/ (click the "Enjoy life" button on the page) for a version that you can run instantly without downloading anything. If you want to download and seriously play with TGOL, check out the open-source Life simulation software called Golly. It is available for Windows, Linux and Mac at http://golly.sourceforge.net/. Alternatively, if you are the programmer sort, you might even venture 10 minutes into making a rough Life simulator yourself (like I first did few years ago)
TGOL simulations can be executed by defining a starting pattern. It can be as complex as you want or as simple as you want. TGOL develops many interesting patterns that people have actually named a lot of them. However, new patterns are found all the time and it seems Life never gets boring! A wonderful place to start on the patterns and their details would be the Life page at http://www.math.com/students/wonders/life/life.html. Try the Glider or Spaceship patterns - they move and were among the first simple-yet-complex emergent entities to be spotted in the TGOL!
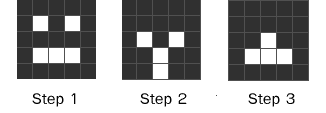
Here are 3 steps in the operation of a crude smiley pattern in TGOL:
Complexity
After playing around with different patterns and observing what happens after a few thousand or few hundred thousand generations in the TGOL universe, it becomes apparent that different sorts patterns get created along the way. Some are dynamic (like the Gliders), some are still, some are oscillatory, some go on seemingly expanding and growing, some develop motion to either of the sides. These more complex structures can occur frequently and regularly and even arrange themselves to form even more complex systems and behaviour.
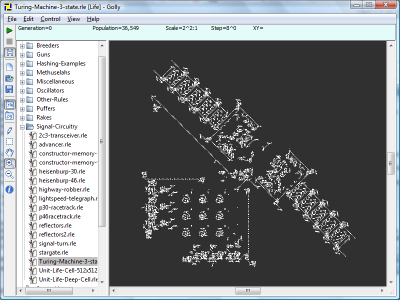
If you are using Golly, look under "Signal Circuitry" for a pattern called "Turing Machine". As anyone whose studied computer science may know, a Turing machine can perform just about any computation. The fact that a Turing machine can be implemented in the TGOL demonstrates the sheer power that a world operated by a few simple rules could posses. More complex patterns are still being discovered within this universe of the TGOL which is dictated by 3 simple rules. The active universe in a TGOL simulation quickly becomes larger than what most computers can currently handle and does limit our ability to further observe the kind of even more complex behaviour TGOL produces.
Like I said at the beginning, The Game of Life is one of the simplest Cellular Automata around. There are many different kinds of cellular automata, each operating with a different number of states and rules. These produce an even richer variety of universes, displaying amazing complexity.
The End
Hopefully this little incursion into emergent complexity was enough to make you think just how likely it is that this "complex" world which we are both puzzled and fascinated by could have arisen from a really really simple set of rules - like the physical/chemical rules that govern everything in the universe.
Introduction
Enter John Conway's "The Game of Life" - one of the simplest examples of emergent complexity. The Game of Life (hereafter abbreviated to TGOL) is a type of cellular automata. Cellular Automata can be defined as a structure (cell) which has a finite set of states and any transitions from one state to another occur according to a set of predetermined rules. TGOL operates in a universe represented by a 2-dimensional grid - where the state of each cell in the grid is boolean; i.e. a cell is either alive or dead. The rules, in TGOL, simply determine the state of a cell at any given moment in time as per the states of the cells surrounding it. That's as much complexity as there is in TGOL (and many other Cellular Automata)!
It is quite intuitive to imagine this working at small scales for just a few steps in time but it quickly gets a bit too large a problem to work out in the head. In fact, TGOL can only be executed effectively using the massive computational abilities of a computer but even then, after sometime, the problem gets beyond which a computer can handle. What more, it is near impossible to determine the future state of the cells based on the starting states.
Experiment!
First, the "rules" in The Game of Life as defined by Conway.
- Any dead cell becomes alive if it has exactly 3 live neighbours.
- Any live cell with either 2 or 3 live neighbours stay alive.
- Any other case either kills the cell if it's alive or leaves it dead if it's already dead.
You can "play" TGOL on paper or simulate it on the computer. Being the lazy people we are, I have no doubt most of you would choose the latter option - but if you are any bit curious about TGOL, do try working it out manually first. There are many Life simulation programs available for free on the net - some are run online while some are available for download. Try the Java based Life simulator at http://www.ibiblio.org/lifepatterns/ (click the "Enjoy life" button on the page) for a version that you can run instantly without downloading anything. If you want to download and seriously play with TGOL, check out the open-source Life simulation software called Golly. It is available for Windows, Linux and Mac at http://golly.sourceforge.net/. Alternatively, if you are the programmer sort, you might even venture 10 minutes into making a rough Life simulator yourself (like I first did few years ago)
TGOL simulations can be executed by defining a starting pattern. It can be as complex as you want or as simple as you want. TGOL develops many interesting patterns that people have actually named a lot of them. However, new patterns are found all the time and it seems Life never gets boring! A wonderful place to start on the patterns and their details would be the Life page at http://www.math.com/students/wonders/life/life.html. Try the Glider or Spaceship patterns - they move and were among the first simple-yet-complex emergent entities to be spotted in the TGOL!
Here are 3 steps in the operation of a crude smiley pattern in TGOL:

Complexity
After playing around with different patterns and observing what happens after a few thousand or few hundred thousand generations in the TGOL universe, it becomes apparent that different sorts patterns get created along the way. Some are dynamic (like the Gliders), some are still, some are oscillatory, some go on seemingly expanding and growing, some develop motion to either of the sides. These more complex structures can occur frequently and regularly and even arrange themselves to form even more complex systems and behaviour.
If you are using Golly, look under "Signal Circuitry" for a pattern called "Turing Machine". As anyone whose studied computer science may know, a Turing machine can perform just about any computation. The fact that a Turing machine can be implemented in the TGOL demonstrates the sheer power that a world operated by a few simple rules could posses. More complex patterns are still being discovered within this universe of the TGOL which is dictated by 3 simple rules. The active universe in a TGOL simulation quickly becomes larger than what most computers can currently handle and does limit our ability to further observe the kind of even more complex behaviour TGOL produces.
Like I said at the beginning, The Game of Life is one of the simplest Cellular Automata around. There are many different kinds of cellular automata, each operating with a different number of states and rules. These produce an even richer variety of universes, displaying amazing complexity.
The End
Hopefully this little incursion into emergent complexity was enough to make you think just how likely it is that this "complex" world which we are both puzzled and fascinated by could have arisen from a really really simple set of rules - like the physical/chemical rules that govern everything in the universe.